sem优化专员_网易企业邮箱客服_关键词优化报价推荐_手机百度网盘下载慢怎么解决

/*** Definition for singly-linked list.* struct ListNode {*     int val;*     ListNode *next;*     ListNode() : val(0), next(nullptr) {}*     ListNode(int x) : val(x), next(nullptr) {}*     ListNode(int x, ListNode *next) : val(x), next(next) {}* };*/
class Solution {
public:ListNode* mergeTwoLists(ListNode* list1, ListNode* list2) {//迭代写法ListNode* dummy = new ListNode(0);ListNode* head = dummy;if(list1 == nullptr) return list2;if(list2 == nullptr) return list1;while(list1 != nullptr && list2 != nullptr){if(list1->val > list2->val){dummy->next = list2;list2 = list2->next;}else{dummy->next = list1;list1 = list1->next;}dummy = dummy->next;}if(list1 == nullptr){dummy->next = list2;}else{dummy->next = list1;}return head->next;}
};

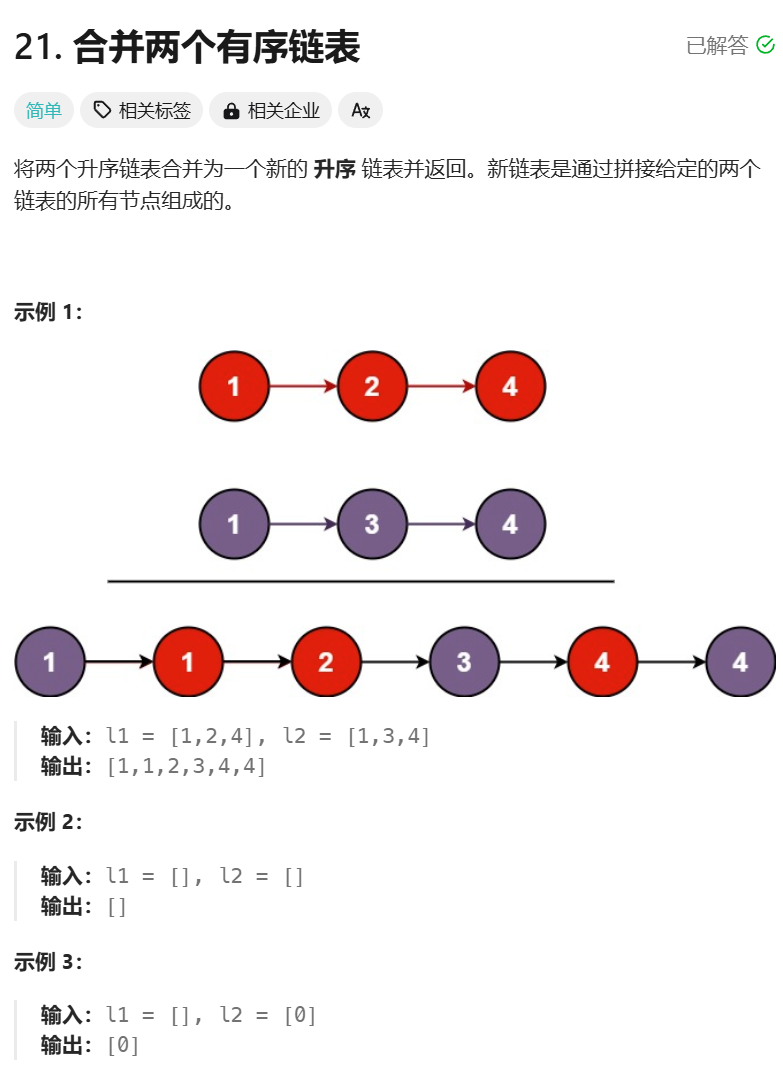
今天复习的是合并链表系列，合并2个链表简单题不再赘述。

有一个非常唐的做法就是依次两两合并K个链表。

/*** Definition for singly-linked list.* struct ListNode {*     int val;*     ListNode *next;*     ListNode() : val(0), next(nullptr) {}*     ListNode(int x) : val(x), next(nullptr) {}*     ListNode(int x, ListNode *next) : val(x), next(next) {}* };*/
class Solution {
public:ListNode* mergeKLists(vector<ListNode*>& lists) {int len = lists.size();if(len == 0) return nullptr;if(len == 1) return lists[0];ListNode* curr = new ListNode(0);curr = lists[0];for(int i = 1; i<len;i++){curr = mergeTwoLists(curr,lists[i]);}return curr;}ListNode* mergeTwoLists(ListNode* l1,ListNode* l2) {if(l1 == nullptr) return l2;if(l2 == nullptr) return l1;if(l1->val <= l2->val){l1->next = mergeTwoLists(l1->next,l2);return l1;}else{l2->next = mergeTwoLists(l1,l2->next);return l2;}}
};

然而我们可以用分治来优化上面这种解法：

class Solution {
public:ListNode* mergeKLists(vector<ListNode*>& lists) {return MergeKLists(lists, 0, lists.size()-1);}ListNode* MergeKLists(vector<ListNode*>& lists, int l, int r){if (l > r) return nullptr;if (l == r) return lists[l];int mid = l + (r - l) / 2;auto left = MergeKLists(lists, l, mid);auto right = MergeKLists(lists, mid+1, r);return MergeTwoLists(left, right);}ListNode* MergeTwoLists(ListNode* l1, ListNode* l2){ListNode* dummy = new ListNode();ListNode* cur = dummy;while (l1 != nullptr && l2 != nullptr) {if (l1->val < l2->val) {cur->next = l1;l1 = l1->next;} else {cur->next = l2;l2 = l2->next;}cur = cur->next;}cur->next = l1 != nullptr ? l1 : l2;return dummy->next;}
};

这个是把O（n）优化成了O（log2n），一个一个合并是顺序遍历，分治来做的话让他自己内部合并，而不用像遍历一样去维护一个ans。还有一个方法是用最小堆来做，也是容易想到的，所以这道题目应该不算是困难题。

/*** Definition for singly-linked list.* struct ListNode {*     int val;*     ListNode *next;*     ListNode() : val(0), next(nullptr) {}*     ListNode(int x) : val(x), next(nullptr) {}*     ListNode(int x, ListNode *next) : val(x), next(next) {}* };*/
class Solution {
public:ListNode* sortList(ListNode* head) {if(head == nullptr || head->next == nullptr){return head;}ListNode* mid = findMiddle(head);ListNode* rightHead = mid->next;mid->next = nullptr;ListNode* l1 = sortList(head);ListNode* l2 = sortList(rightHead);return mergeTwoLists2(l1,l2);}ListNode* findMiddle(ListNode* head) {ListNode* slow = head;ListNode* fast = head->next;while(fast != nullptr && fast->next != nullptr){slow = slow->next;fast = fast->next->next;}return slow;}//合并有序链表1ListNode* mergeTwoLists(ListNode* l1,ListNode* l2){ListNode* dummy = new ListNode(0);ListNode* curr = dummy;while(l1 != nullptr && l2 != nullptr){if(l1->val > l2->val){curr->next = l2;l2 = l2->next;}else if(l1->val <= l2->val){curr->next = l1;l1 = l1->next;}curr = curr->next;        }if(l1 == nullptr){curr->next = l2;}else{curr->next = l1;}return dummy->next;}//合并有序链表2ListNode* mergeTwoLists2(ListNode* l1,ListNode* l2){if(l1 == nullptr){return l2;}if(l2 == nullptr){return l1;}if(l1->val > l2->val) {l2->next = mergeTwoLists2(l1,l2->next);return l2;}else{l1->next = mergeTwoLists2(l1->next,l2);return l1;}}
};

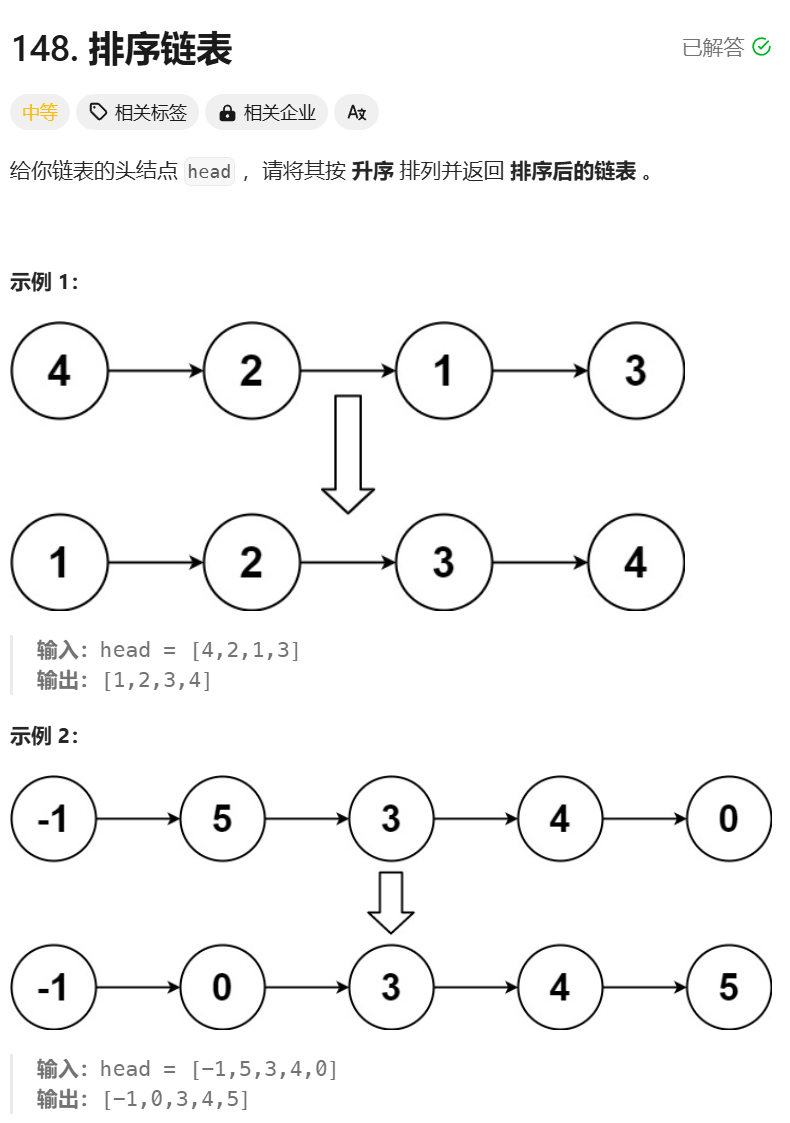
  这实际上也是分治（归并排序）。归并给我的感觉就像是你很难处理一个棘手的问题，然后你把这个棘手的问题一步步拆解下放，直到你能解决的地步，比如这里对于链表排序就是拆解到只剩下两个节点的时候，你肯定能通过判断大小关系直接排序了，然后一步步回升，直到解决这个问题。

  这里有个工具函数，找链表中点我们可以记忆一下。这是一个快慢指针，这个判断条件你可以画图证明一下，如果节点总数是偶数，最后fast->next == nullptr。如果节点总数是奇数，最后fast == nullptr。都是比较好证明的。

OK，今天看的这几道题都不是很难，后面两道用到了归并的思想。